
Overview
Modern machine learning has moved towards leveraging large models as priors for downstream tasks. For example, we have large language models (LLMs) in natural language processing and large-scale self-supervised representation learning in computer vision. How to build large models as good priors for solving reinforcement learning (RL) problems? One promising direction is to learn a prior over the policies of some yet-to-be-determined tasks: prefetch as much computation as possible before a specific reward function is known.
Recent work (forward-backward (FB) representation learning) has tried this, arguing that an unsupervised representation learning procedure can enable optimal control over arbitrary rewards without further fine-tuning. Conceptually, this idea resembles the in-context learning in LLMs. However, this formulation results in a circular dependency between learned representations and policies (see the figure above), incurring optimization challenges. In this work, we demystify FB by clarifying when such representations can exist, what its objective optimizes, and how it converges in practice.
Our analysis suggests a simplified unsupervised pre-training method for RL that breaks the circular dependency (see the figure above): one-step forward-backward representation learning (one-step FB). Instead of enabling optimal control, one-step FB performs one step of policy improvement.
Demystifying Forward-Backward Representation Learning
Forward-backward representation learning factorizes successor measures of the current policies into bilinear representations, and uses those representations to acquire new policies. Touati & Ollivier implicitly assumes that, in discrete controlled Markov processes (CMPs; Markov decision processes without a reward function), a ground-truth (oracle) factorization exists and the practical FB algorithm can converge to it. We want to both theoretically and empirically understand whether these assumptions hold for FB. Therefore, we aim to answer the following questions in our analysis.
When do the ground-truth FB representations exist? In discrete CMPs, we find four necessary conditions for the existence of ground-truth FB representations: Click to see the four necessary conditions.
- representation dimension \( d \): \( d \geq \left| \mathcal{S} \times \mathcal{A} \right| \).
- rank of the ground-truth forward representation matrix \( F_{\mathcal{Z}}^{\star} \): \( \left| \mathcal{S} \times \mathcal{A} \right| \leq \text{rank}(F_{\mathcal{Z}}^{\star}) \leq d \).
- rank of the ground-truth backward representation matrix \( B^{\star} \): \( \text{rank}(B^{\star}) = d \).
- relationship between the ground-truth forward-backward representation matrices and successor measures \( M^{\pi}( a \mid s, z) \): $$ B^{\star} = F^{\star +}_{z_1} M^{\pi(a \mid s, z_1)} / \rho = \dots = F^{\star +}_{z_{|\mathcal{Z}|}} M^{\pi( a \mid s, z_{|\mathcal{Z}|})} / \rho, $$ where \(X^{+}\) denotes the pseudoinverse of the matrix \(X\).
What does the FB representation objective minimize? We interpret the representation objective in FB as a temporal-difference (TD) variant of the least-squares importance fitting (LSIF) loss, drawing a connection to fitted Q-evaluation (FQE). FQE performs approximate value iteration, which (approximately) enjoys convergence guarantee. This connection motivates us to study whether FB admits a similar convergence in practice.
Does the practical FB algorithm converge to ground-truth representations? We define a new FB Bellman operator to answer this question. Unfortunately, the FB Bellman operator is not a \(\gamma\)-contraction, suggesting that the Banach fixed-point theorem fails to apply.
In theory, whether the FB algorithm converges to any ground-truth representations remains an open problem. The key challenge comes from the circular dependency between the FB representations and the policies. In practice, we will use didactic experiments to demonstrate the failure convergence of FB.
A Simplified Algorithm for Unsupervised Pre-training in RL
Our understanding of FB reveals that its inherent circular dependency incurs optimization challenges and unclear learning behaviors. To break the circular dependency, we propose a simplified pre-training method for RL called one-step forward-backward (one-step FB) representation learning.
- Instead of learning FB representations for the current policy, one-step FB learns representations for a fixed behavioral policy \( \pi_{\beta} \).
- Unlike FB, which argues to prefetch optimal controls for arbitrary reward functions, one-step FB performs policy adaptation via one step of policy improvement.
- Empirically, we find that one-step FB enjoys clear convergence in didactic discrete CMPs and achieves comparable zero-shot performance against FB on standard offline RL benchmarks.
- Starting from the existing FB algorithm, implementing our method requires making two simple changes.
- Remove the latent variable from the input to the forward representation.
- In the representation loss, sample the next action from the dataset instead of the target policy.

Experiments on Standard Benchmarks
Domains
- We select a set of \(4\) state-based domains from the ExORL benchmark.
- We also select a set of \( 6 \) state- and image-based domains from the OGBench benchmark.
- While pre-training a set of policies using each algorithm, we measure the performance of zero-shot policy adaptation to downstream tasks (\(16\) tasks from ExORL and \(30\) tasks from OGBench).
Offline zero-shot RL
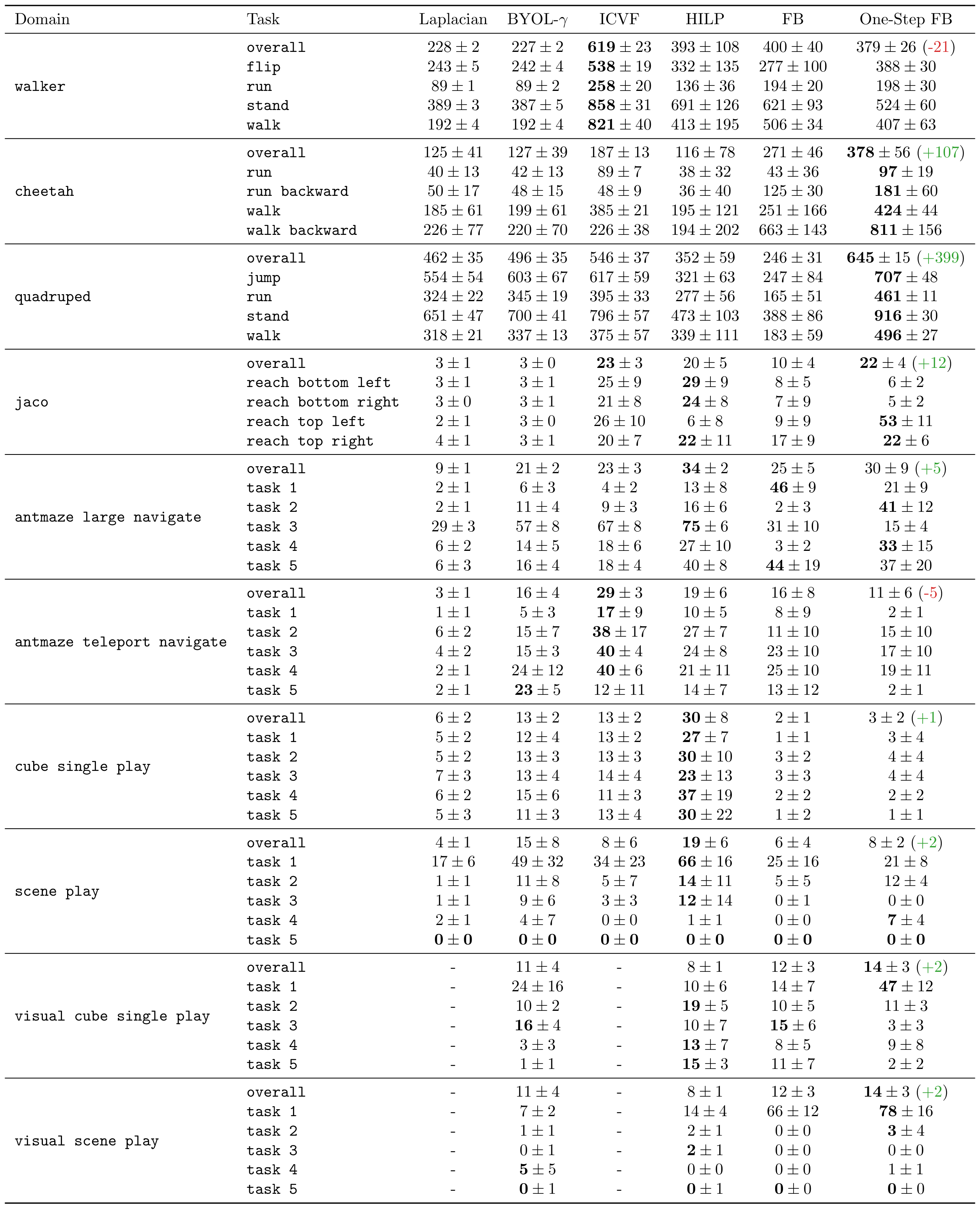
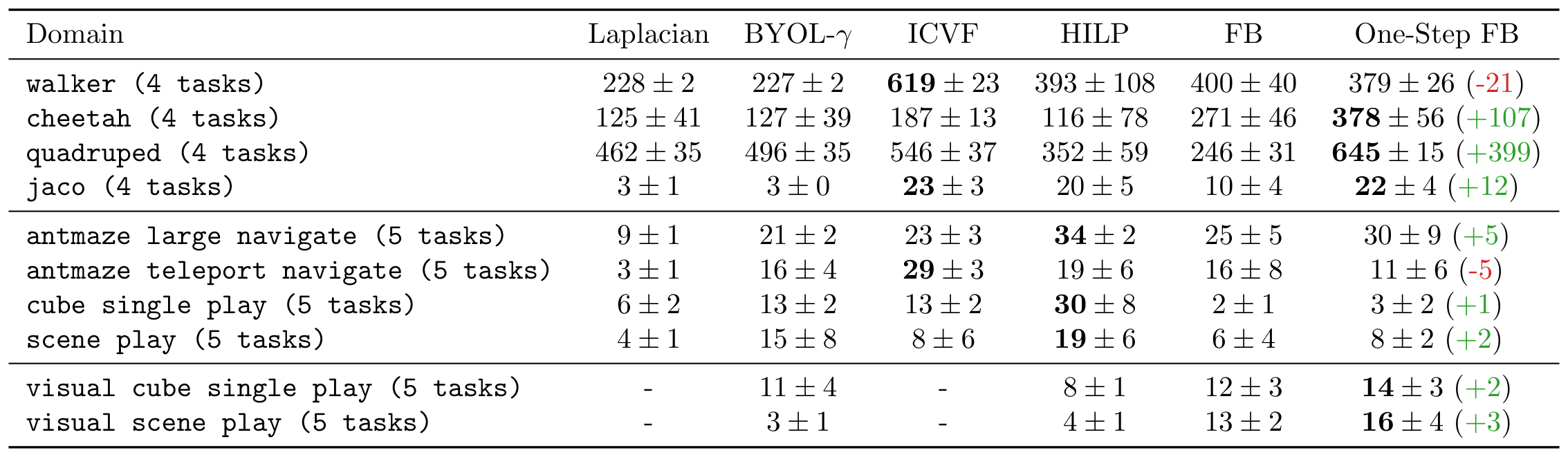
- One-step FB achieves the best or near-best performance on \( 6 \) out of \( 10 \) domains.
- Compared with FB, one-step FB achieves \(+1.4 \times\) improvement on average.
- One-step FB is able to outperform prior methods by \(20\%\) using RGB images directly.
Offline-to-online fine-tuning

- After offline unsupervised pre-training, we conduct online fine-tuning of the policies pre-trained by different methods using the same off-the-shelf RL algorithm (TD3).
- One-step FB continues to provide higher sample efficiency (\(+40\%\) on average) during fine-tuning, as compared with the original FB method.
- The fine-tuned policies reach the asymptotic performance of TD3 at the end of training.
The Key Components of One-Step FB


BibTeX
@article{zheng2026can,
title={Can We Really Learn One Representation to Optimize All Rewards?},
author={Zheng, Chongyi and Jayanth, Royina Karegoudra and Eysenbach, Benjamin},
journal={arXiv preprint arXiv:2602.11399},
year={2026},
}